1. 默克尔树
Merkle 树的叶子是数据块的 hash 值。非叶节点是其对应子节点串联字符串的 hash。
如下图所示,A、B、C、D是数据块,H()代表哈希函数。
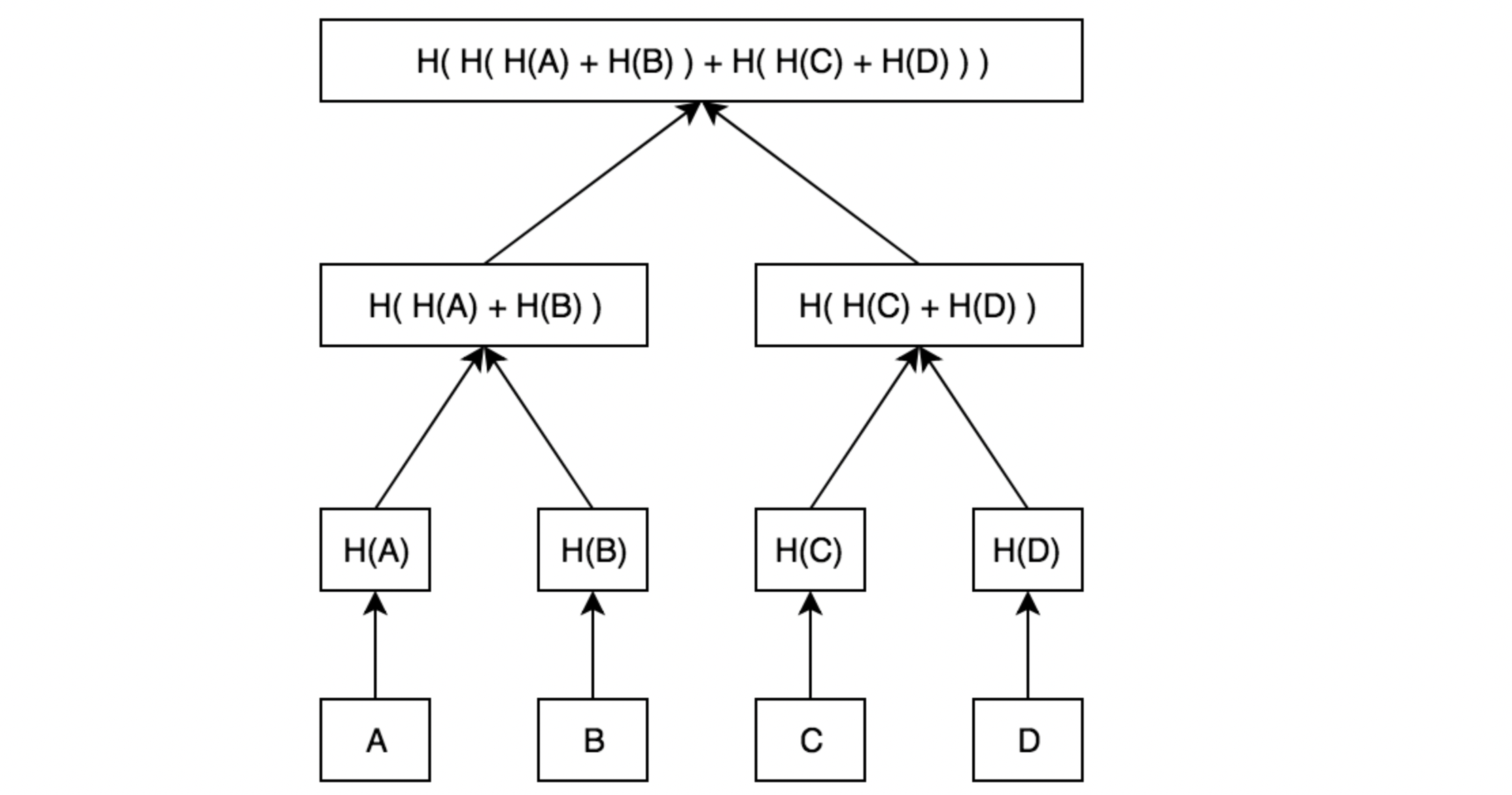
1.1. 默克尔树的存在证明
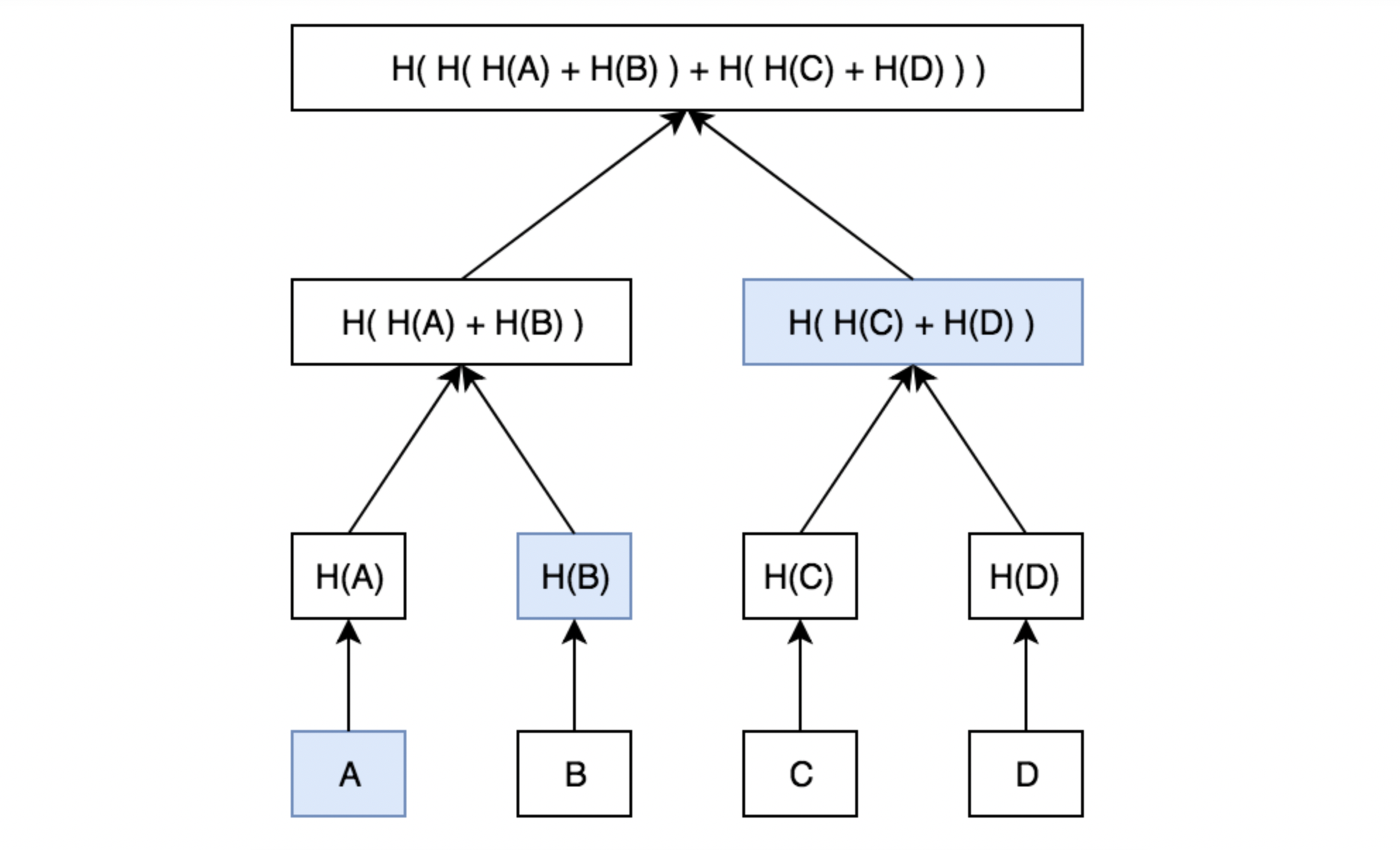
默克尔树的存在证明,也叫做默克尔证明,这些证明能够表明一个叶节点是默克尔树的一部分。
例如,为了证明数据A(严格来说是A的哈希H(A))存在于此默克尔树中,只需要给出H(B)和H(H(C)+H(D)),就可以计算出根哈希,然后和原根哈希一比较即可。
1.2. 默克尔树的不存在证明
不太容易实现。
2. 稀疏默克尔树
稀疏默克尔树(Sparse Merkle Tree,SMT)与默克尔树基本类似,只是数据是有序的。
例如有一个四个叶子节点的SMT,然后有数据A和D,那么这SMT如下:
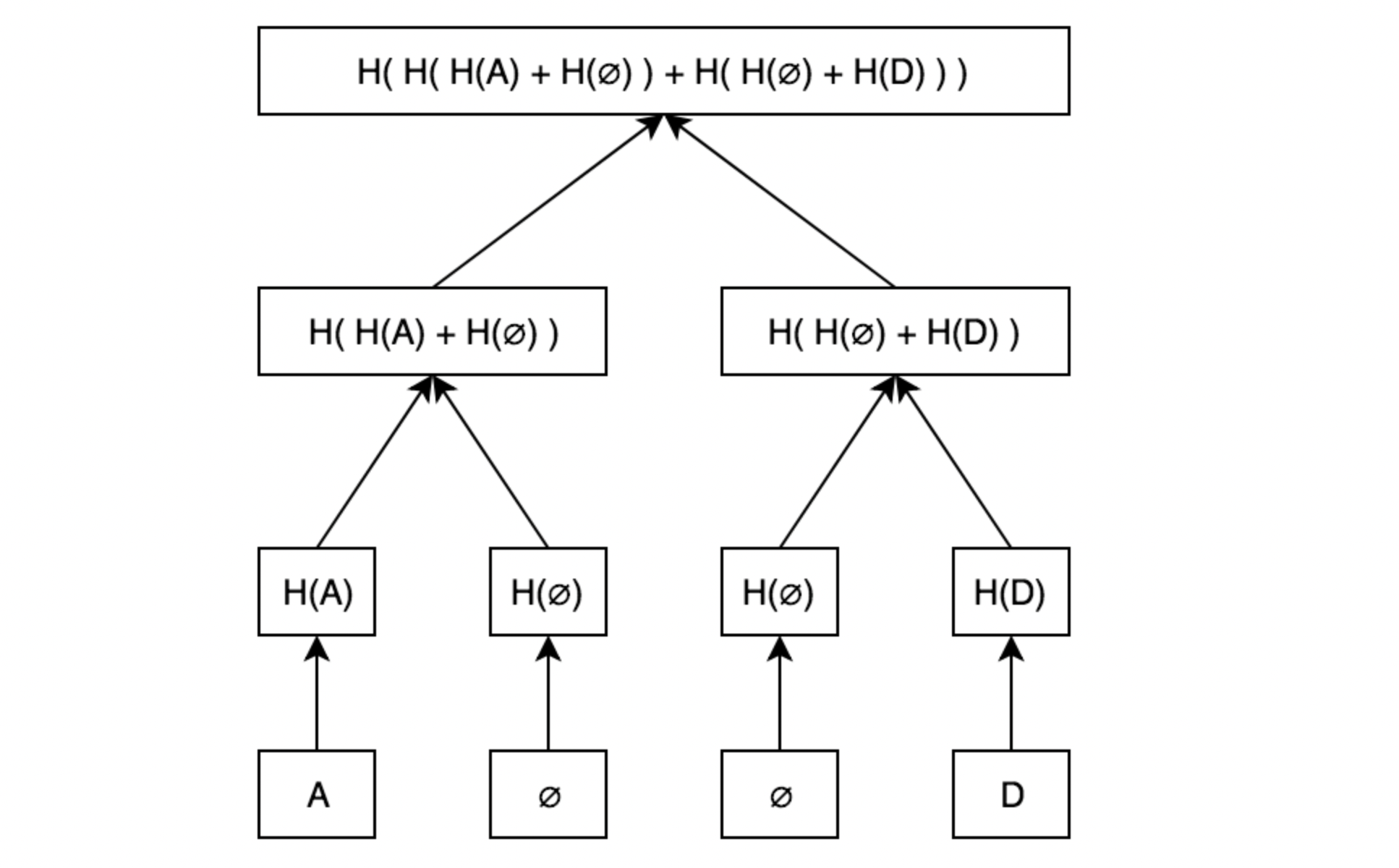
可以看到,A和D被有序的放到了索引是0和3的位置,而所以是1和2的位置是null。
2.1. 稀疏默克尔树的存在证明
与默克尔树的存在证明一致,只需要给出H(null)和H(H(null)+H(D))。
且SMT的值可以在O(log(n)) 时间内进行更新、插入或删除操作。
2.2. 稀疏默克尔树的不存在证明
与默克尔树最大的区别在于,稀疏默克尔树可以方便的实现不存在证明。
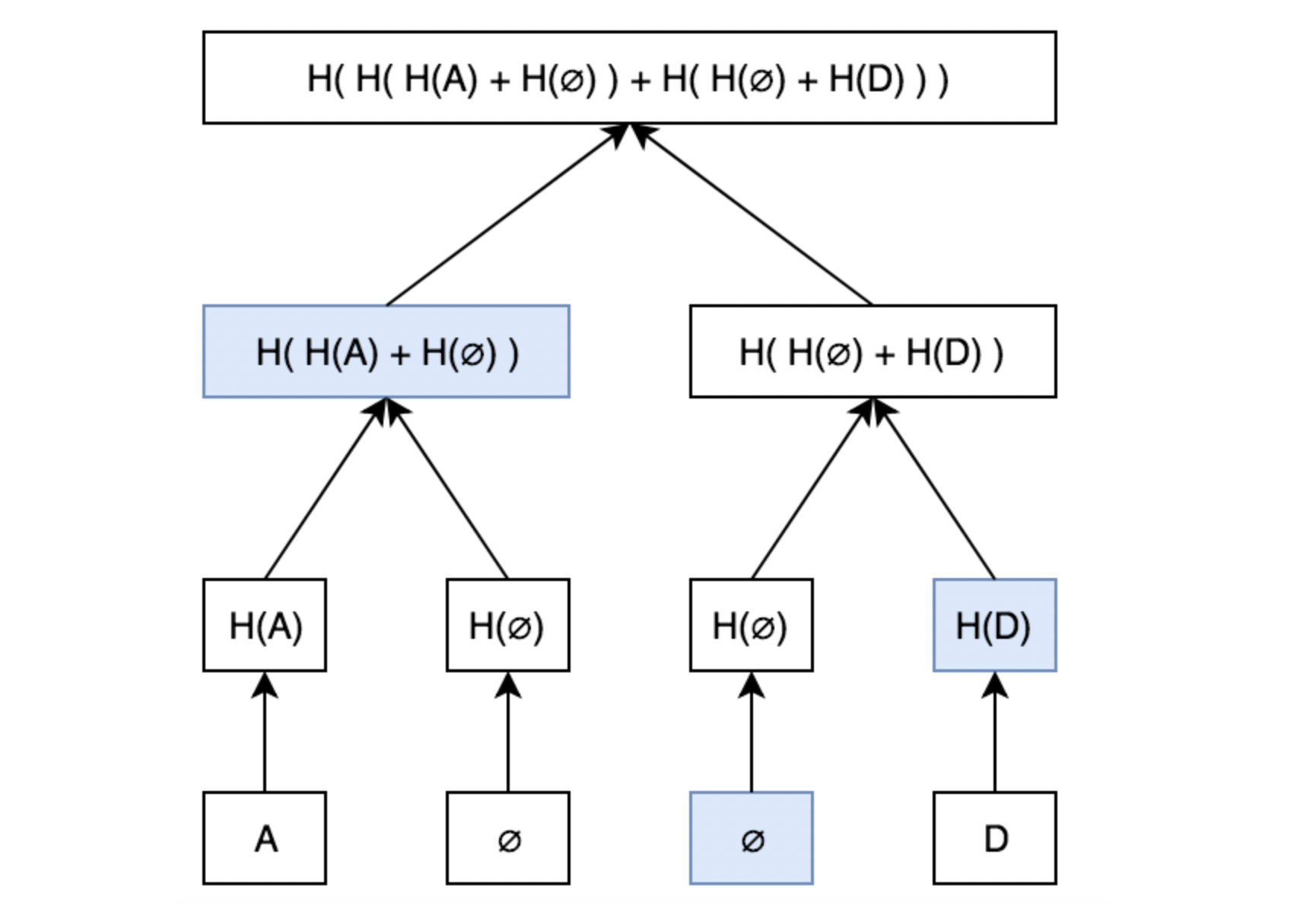
例如需要证明C不存在,那么只需证明索引3处是null即可,也就转化为常规的默克尔证明,只需给出H(H(A)+H(null))和H(D),如下图所示: